#include <small_world_graph_builder.h>

Inheritance diagram for fpmas::graph::SmallWorldGraphBuilder< T >:

Collaboration diagram for fpmas::graph::SmallWorldGraphBuilder< T >:

Public Member Functions
	SmallWorldGraphBuilder (float p, std::size_t k)

std::vector< api::graph::DistributedNode< T > * >	build (api::graph::DistributedNodeBuilder< T > &node_builder, api::graph::LayerId layer, api::graph::DistributedGraph< T > &graph) override

virtual std::vector< api::graph::DistributedNode< T > * >	build (DistributedNodeBuilder< T > &node_builder, LayerId layer, DistributedGraph< T > &graph)=0

Detailed Description

template<typename T>
class fpmas::graph::SmallWorldGraphBuilder< T >

A distributed procedure to build Small World graphs, inspired from the work of Duncan J. Watts and Steven H. Strogatz. The original procedure as been adapted to support directed graphs.

We consider a node count N, a mean output degree K (supposed to be even), and a probability p.

Build N nodes, and connect them in a CYCLE as specified in the RingGraphBuilder. K/2 is used as a parameter for the RingGraphBuilder, so that each node as K outgoing neighbors in total (K/2 on each side).
Consider each edge, and select it for rewiring with a probability p. If selected, chose if target or source will be rewired with a probability 0.5.
Rewires all edges that need a new target. The new target is chosen randomly among all the nodes. Nothing is done if the randomly selected new target corresponds to the current source, of if an edge already exists from the current source to the selected target.
Synchronization barrier
Analog procedure for all edges that need a new source.

Explanations

It is necessary to randomly chose which side of each edge to rewire, to prevent all nodes to have exactly K outgoing neighbors at the end of the process.
The synchronization barrier prevents concurrency issues. For example, during step 3, it is not possible for any process other that the current one to build a new outgoing edge from the current source, since only new targets are selected, so that it is safe to check for existing outgoing edges.

Example

	n=16, k=4, p=0.1
Global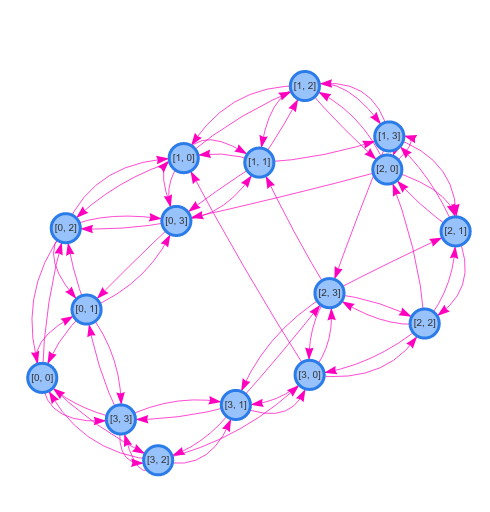
Distributed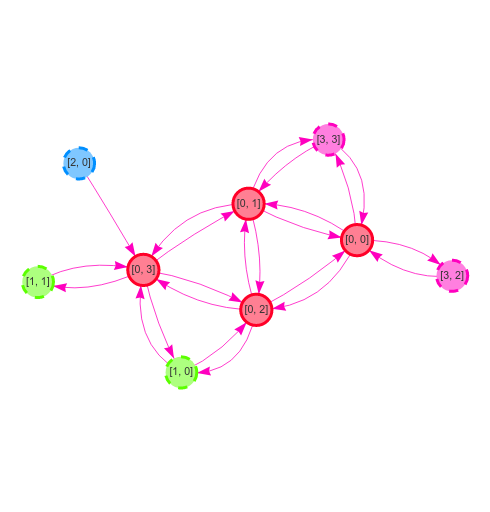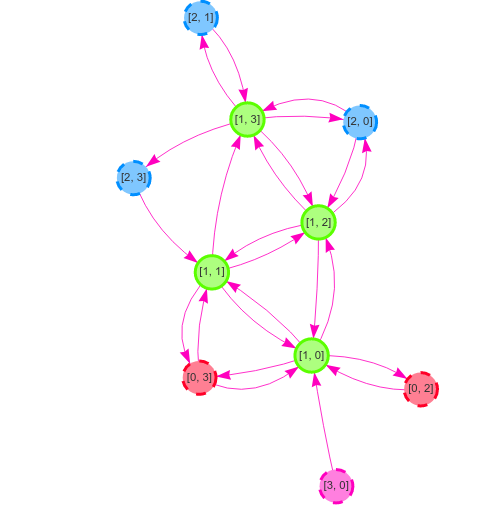
Distributed

Constructor & Destructor Documentation

◆ SmallWorldGraphBuilder()

template<typename T >

fpmas::graph::SmallWorldGraphBuilder< T >::SmallWorldGraphBuilder	(	float	p,
		std::size_t	k
	)

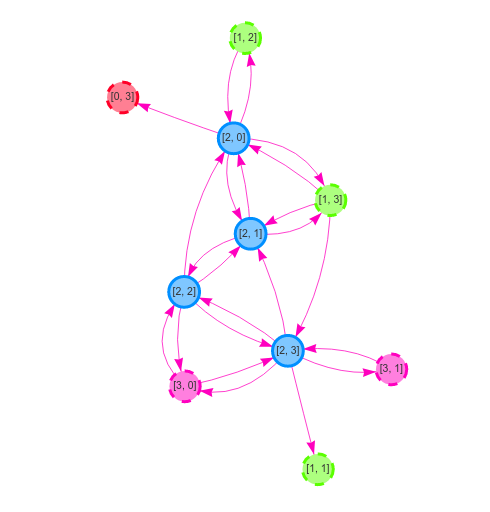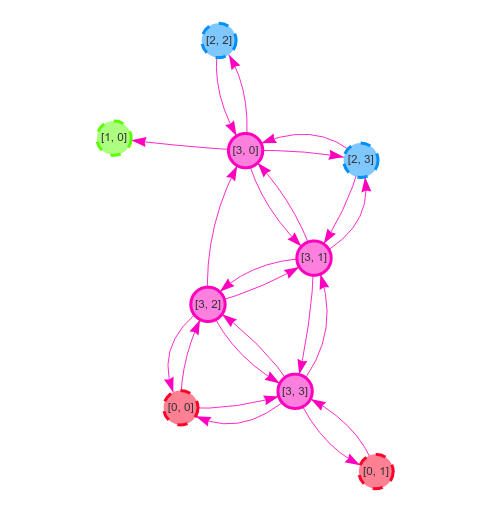inline

SmallWorldGraphBuilder constructor.

Notice that the node count is deduced from the count of nodes available in the node builder passed to the build() method.

In order to respect the Small World assumptions, it is supposed that k is even and N >> k >> ln(N). With p=0, the graph will be perfectly regular, with p=1, it will be completely random. In practice, low values of p (like p=0.1) are enough to expose the small world properties without falling in a completely random graph. The intuitive reason for that is that the idea of random rewiring is to create some shortcuts across the original ring to reduce distance from initially far nodes, and only a few are required to globally reduce lengths of paths in the graph, while preserving a high clustering coefficient.

The build process uses the RandomGraphBuilder::distributed_rd, so the process can be seeded with RandomGraphBuilder::seed() or fpmas::seed().

Parameters

p	probability of rewriring each edge
k	initial output degree of each node (assumed to be even)

Member Function Documentation

◆ build()

template<typename T >

std::vector< api::graph::DistributedNode< T > * > fpmas::graph::SmallWorldGraphBuilder< T >::build	(	api::graph::DistributedNodeBuilder< T > &	node_builder,
		api::graph::LayerId	layer,
		api::graph::DistributedGraph< T > &	graph
	)

overridevirtual

Automatically builds the specified graph according to the current implementation.

Nodes are generated using the specified DistributedNodeBuilder. More precisely, DistributedNodeBuilder::localNodeCount() nodes will be inserted in the graph. Generated nodes can then be linked on the specified layer, according to rules defined by the implemented algorithm.

Notice that the specified graph is not required to be empty.

Contrary to the GraphBuilder, this process is synchronous and should be called from all processes.